[笔记]花花酱LeetCode SP
数据结构特辑
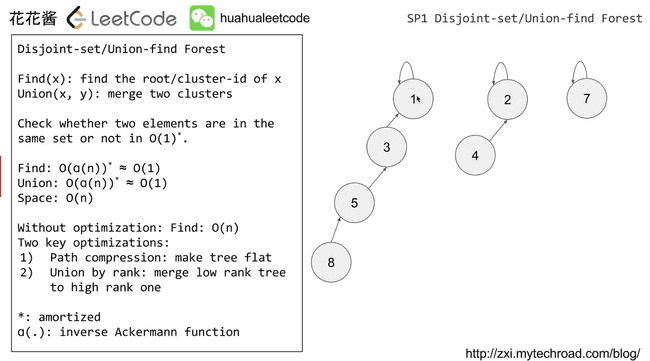
SP1 Disjoint-set/Union-find Forest
Check whether two elements are in the same set or not in O(1)
method
Finc(x): find the root/cluster-id of x
Union(x, y): merge two clusters
Find: O(1)
Union: O(1)
without optimization: Find O(n)
Two key optimizations:
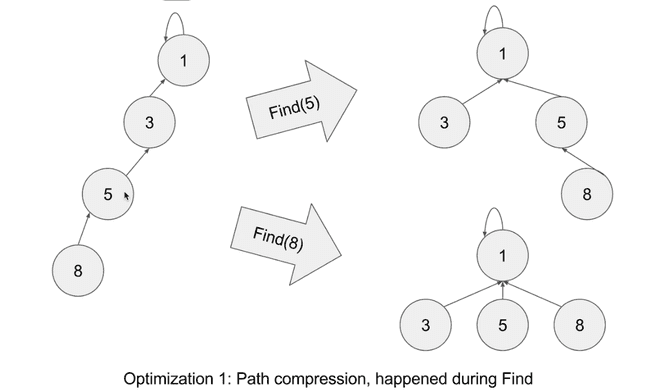
1) Path compression: make tree flat
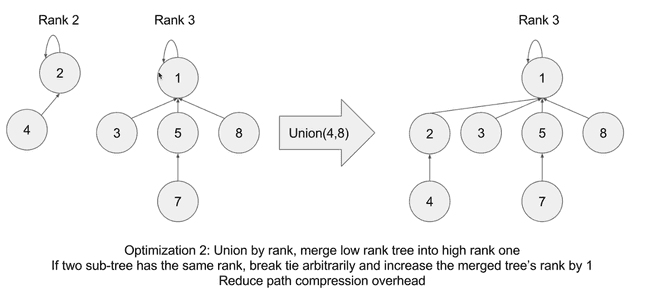
2) Union by rank: merge low rank tree to high rank onepath compression
path compression happend during Find
union by rank
merge low rank tree into high rank one in union
Pseudo code
class UnionFindSet:
func UnionFindSet(n):
parents = [1..n] // 数组
ranks = [0..0] (n zeros) // 数组
func Find(x):
if x != parents[x]:
parents[x] = Find(parents[x])
return parents[x]
func Union(x, y):
px, py = Find(x), Finx(y)
if rank[px] > rank[py]: parents[py]=px
if rank[px] < rank[py]: parents[px]=py
if rank[px] == rank[py]:
parents[py]=px
rank[px]++
class UnionFind:
def __init__(self, n):
self.parent = list(range(n)) # 初始时每个节点的父节点是自己
self.rank = [0] * n # 初始时每个节点的秩都是0
def find(self, x):
if x != self.parent[x]:
self.parent[x] = self.find(self.parent[x]) # 路径压缩
return self.parent[x]
def union(self, x, y):
px, py = self.find(x), self.find(y)
if px == py: # 已经在同一集合中
return
if self.rank[px] > self.rank[py]:
self.parent[py] = px
elif self.rank[px] < self.rank[py]:
self.parent[px] = py
else:
self.parent[py] = px
self.rank[px] += 1
def connected(self, x, y):
return self.find(x) == self.find(y)
# 创建包含5个节点的并查集
uf = UnionFind(5)
# 合并节点
uf.union(0, 1) # 合并0和1
uf.union(2, 3) # 合并2和3
uf.union(1, 2) # 合并1和2(同时会连接0,1,2,3)
# 检查连通性
print(uf.connected(0, 3)) # True
print(uf.connected(0, 4)) # Falsego impl
type UnionFindSet struct {
parents []int
ranks []int
}
func NewUnionFindSet(n int) *UnionFindSet {
ufs := &UnionFindSet{
parents: make([]int, n+1),
ranks: make([]int, n+1),
}
for i := 0; i < len(ufs.parents); i++ {
ufs.parents[i] = i
}
return ufs
}
func (ufs *UnionFindSet) Union(u, v int) bool {
pu := ufs.Find(u)
pv := ufs.Find(v)
if pu == pv {
return false
}
if ufs.ranks[pv] < ufs.ranks[pu] {
ufs.parents[pv] = pu
} else if ufs.ranks[pu] < ufs.ranks[pv] {
ufs.parents[pu] = pv
} else {
ufs.parents[pv] = pu
ufs.ranks[pu] += 1
}
return true
}
func (ufs *UnionFindSet) Find(u int) int {
if u != ufs.parents[u] {
ufs.parents[u] = ufs.Find(ufs.parents[u])
}
return ufs.parents[u]
}Leetcode
737 Sentence Similarity II
684 Redundant Connection
547 Friend Circles
Union-Find Problems:
* LeetCode 399. Evaluate Division https://youtu.be/UwpvInpgFmo
* LeetCode 547. Friend Circles https://youtu.be/HHiHno66j40
* LeetCode 737. Sentence Similarity II https://www.youtube.com/watch?v=0rZUi3kZGLI
* LeetCode 684. Redundant Connection https://www.youtube.com/watch?v=4hJ721ce010
* LeetCode 685. Redundant Connection II https://youtu.be/lnmJT5b4NlM
* LeetCode 839. Similar String Groups https://zxi.mytechroad.com/blog/string/leetcode-839-similar-string-groups/
* LeetCode 959. Regions Cut By Slashes
LeetCode 399. Evaluate Division https://youtu.be/UwpvInpgFmo
LeetCode 547. Friend Circles https://youtu.be/HHiHno66j40
LeetCode 737. Sentence Similarity II https://www.youtube.com/watch?v=0rZUi3kZGLI&t=0s
LeetCode 684. Redundant Connection https://www.youtube.com/watch?v=4hJ721ce010&t=0s
LeetCode 685. Redundant Connection II https://youtu.be/lnmJT5b4NlM
Reference
https://en.wikipedia.org/wiki/Disjoint-set_data_structure https://www.cs.princeton.edu/courses/archive/spring13/cos423/lectures/UnionFind.pdf
https://www.cs.princeton.edu/courses/archive/spring13/cos423/lectures.php
https://zxi.mytechroad.com/blog/data-structure/sp1-union-find-set/
https://zxi.mytechroad.com/blog/hashtable/leetcode-737-sentence-similarity-ii/ 使用 string 作为 union/find 的 key
SP2: Input Size V.S. Time Complexity
n=100 O(n^3)
n=1000 O(n^2)
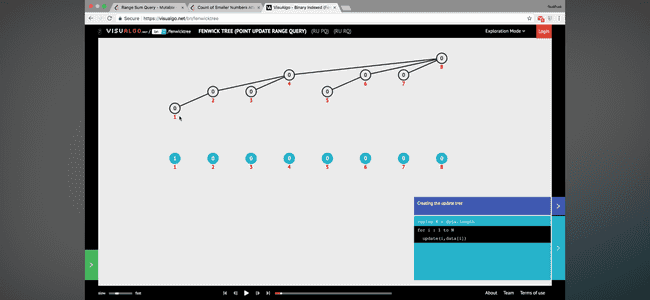
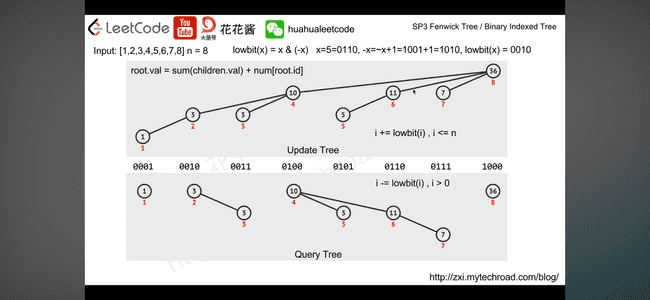
SP3: Fenwick Tree/Binary Indexed Tree
Motivation:
Given a 1D array of n elements: [2, 5, -1, 3, 6]
range sum query: what’s the sum from 2nd element to 4th element query(2,4)? 5+-1+3 = 7
Naive implementation: O(n) per query.
Use DP to pre-compute the prefix sums: O(n) [2, 5, -1, 3, 6] → [2, 7, 6, 9, 15]
reduce query to O(1). query(2, 4) = sums(n1…n4) - sums(n1..n1) = sums[4-1] - sums[1-1] = 9 - 2 =7
What if the values of elements can change? O(n)
Fenwick tree was proposed to solve the prefix sum problem.
The idea is to store partial sum in each node and get total sum by traversing the tree from leaf to root.The tree has a height of log(n)
Query: O(log(n))
Update: O(log(n))
class FenwickTree {
public:
FenwickTree(int n): sums_(n + 1, 0) {}
void update(int i, int delta){
while (i < sums_.size()){
sums_[i] += delta;
i += lowbit(i);
}
}
int query(int i) const {
int sum = 0;
while (i > 0){
sum += sums_[i]
i -= lowbit(i);
}
return sum;
}
private:
static inline int lowbit(int x) { return x & (-x); }
vector<int> sums_;
}Time complexity:
update: O(n)
query: O(n)
Space complexity: O(n)
Applications:
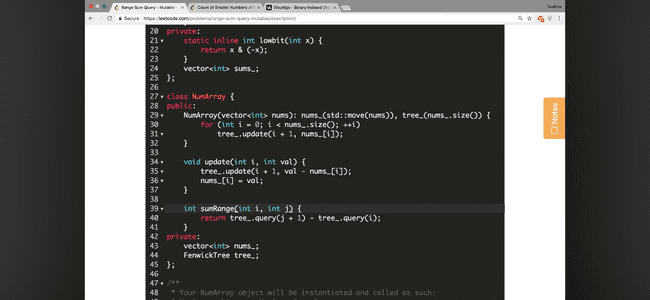
307: Range Sum Query - Mutable
315: Count of Smaller Numbers After Self
SP4: Time/Space Complexity of Recursive Algorithms
master theorem
quick_sort(a, l, r):
p = partition(a, l, r) # O(r-l)
quick_sort(a, l, p)
quick_sort(a, p+1, r)
Bast case:
T(n) = 2*T(n/2) + O(n) = O(nlogn)
Worst case:
T(n) = T(n-1) + T(1) +O(n) = O(n2)
Non-worst cases:
T(n) = T(n/10) + T(9n/10) + O(n) = O(nlogn)
Space Best/Average: O(logn)
Worst: O(n)merge_sort(a, l, r):
m = l + (r - l)/2
merge_sort(a, l, m)
merge_sort(a, m+1, r)
merge_sort(a, l, m, r) # O(r - l)
Time:
T(n) = 2*T(n/2) + O(n) = O(nlogn)
Space:
O(logn + n)binary_search(a, l, r):
m = l + (r - l) / 2
if f(m):
binary_search(a, l, m)
else:
binary_search(a, m+1, r)
Time complexity:
T(n) = T(n/2) + O(1) = O(nlogn)
Space complexity:
O(logn)inorder(root):
inorder(root.left)
func(rool.val)
inorder(root.right)
Time complexity:
T(n) = 2*T(n/2) + O(1) = O(n) perfect
T(n) = T(n-1) + T(1) + O(1) = O(n) worst case
Space complexity:
O(logn) perfect
O(n) worst casecombination(d, s):
if d == n:
return func()
for i in range(s, n):
combination(d+1, i+1)
Time complexity:
T(n) = T(n-1) + T(n-2) + ... + T(1)
= O(2^n)
Space complexity:
O(n)permutation(d, used):
if d == n:
return func()
for i in range(0, n):
if i in used: continue
used.add(i)
permutation(d+1, used)
used.remove(i)
Time complexity:
T(n) = n * T(n-1)
= O(n!)
Space complexity:
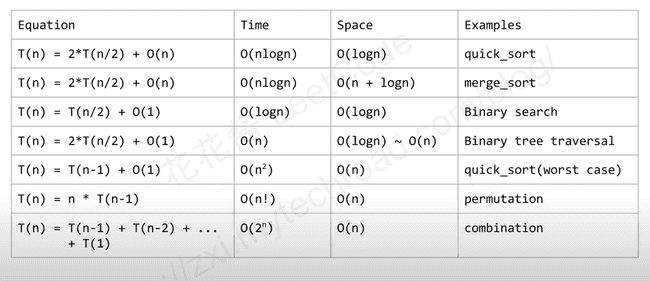
O(n)| Equation | Time | Space | Examples |
|---|---|---|---|
| T(n) = 2*T(n/2) + O(n) | O(nlogn) | O(logn) | quick_sort |
| T(n) = 2*T(n/2) + O(n) | O(nlong) | O(n + logn) | merge_sort |
| T(n) = T(n/2) + O(1) | O(logn) | O(logn) | Binary search |
| T(n) = T(n-1) + O(1) | O(n^2) | O(n) | quick_sort(worst case) |
| T(n) = n * T(n-1) | O(n!) | O(n) | permutation |
| T(n) = T(n-1) + T(n-2) + … T(1) | O(2^n) | O(n) | combination |
DP with memorization
Time: number of subproblems * exclusive time to solve each subproblem
Space: max depth of call stack * space used by each subproblem
fib(n):
if n < 1: return 0
return fib(n-1) + fib(n-2)
T(n) = T(n-1) + T(n-2) + O(1)
= O(2^n)
= O(1.618^n)fib(n):
if n < 1: return 0
if m[n] > 0: return m[n]
m[n] = fib(n-1) + fib(n-2)
return m[n]
n subproblems
each problem takes O(1) to solve
fib(n) takes O(n) time to solveLC 741. Cherry pickup
dp(x1, y1, x2):
if m[x1][y1][x2] != None:
return m[x1][y1][x2]
ans = max(max(dp(...), dp(...)),
max(dp(...), dp(...)))
m[x1][y1][x2] = ans
return m[x1][y1][x2]
n^3 subproblems
Each subproblem takes O(1)
dp(n, n, n) takes O(n^3) to solve
LC 312. Burst Balloons
dp(i, j):
if m[i][j] != None:
return m[i][j]
for k in range(i, j+1):
ans = max(ans, dp(...) + C + dp(...))
m[i][j] = ans
return m[i][j]
n^2 subproblems
Each subproblem takes O(n)
dp(n, n) takes O(n^2) to solveSP5: Binary Search
- What is Binary Search?
- reduce the search space by haft at each step
- input usually needs to be sorted A = [1, 2, 5, 7, 8, 12] exist(A, 7) = True [1, 2, 5, 7, 8, 12] → [7, 8, 12] → [7] exist(A, 9) = False [1, 2, 5, 7, 8, 12] → [7, 8, 12] → [12]
- Why Binary Search?
- Fast
- T(n) = T(n/2) + O(eval)
- O(log(range)) _ O(eval) vs O(range) _ O(eval) linear scan
Range Binary Linear Speed Up (x) 100 7 10 14.29 10000 14 10000 714.29 1000000 20 1000000 50000 1000000000 30 TLE N/A
左闭右开,0 到 n
找到一个最小的 l,使得 g(m)等于 ture
Template:
[l, r)
def binary_search(l, r):
while l < r:
m = l + (r-l)/2
if f(m): return m # optional
if g(m):
r = m # new range [l, m)
else:
l = m+1 # new range [m+1, r)
return l # or not found
Time complexity: O(log(r-l)*(f(m)+g(m)))
Space complexity: O(1)Example 1
return the index of an element in a sorted array. Elements are unique. if not found return -1.
A = [1, 2, 5, 7, 8, 12]
search(8) = 4, search(6) = -1
def binary_search(A, val, l, r):
while l < r:
m = l + (r - l) // 2
if A[m] == val: return m
if A[m] > val:
r = m
else:
l = m + 1
return -1 # not found
binary_search(A, 8, 0, len(A))Example 2
return the lower_bound/upper_bound of a val in sorted array..
lower_bound 大于等于
upper_bound 严格大于
upper_bound - lower_bound 知道重复的元素个数
lower_bound(x): first index of i, such that A[i] ≥ x
upper_bound(x): first index of i, such that A[i] > x
Find the smallest index to satisfy g(index)
def lower_bound(A, val, l, r):
while l < r:
m = l + (r - l)/2
if A[m] >= val: # g(m)
r = m
else:
l = m + 1
return ldef upper_bound(A, val, l, r):
while l < r:
m = l + (r - l) // 2
if A[m] > val: # g(m)
r = m
else:
l = m + 1
return lExample 3: LC 69. |sqrt(x)|
sqrt(4) = 2
sqrt(8) = 2
def sqrt(x):
l = 0
r = x + 1
while l < r:
m = l + (r-l) // 2
if m * m > x:
r = m
else:
l = m + 1
return l - 1 # l*l > xExample 4: LC 278
First Bad Version Interactive problem
bool isBadVersion(int version);
def firstBadVersion(n):
l = 0
r = n
while l < r:
m = l + (r - l) // 2
if isBadVersion(m):
r = m
else
l = m + 1
return lExample 5: LC 875 koko Eating Bananas
Find minimum K such that she can eat all the bananas within H hours.
def eat(piles, H):
l = 1
r = max(piles) + 1
while l<r:
m = l+(r-l)//2
h = 0
for p in piles: # O(n)
h += (p + m - 1) / m
if h <= H # g(m): can finish
r = m
else:
l = m + 1
return lExample 6: LC 378 Kth Smallest Element in a Sorted Matric
Each row and column are sorted.
def KthSmallest(A, k):
l = A[0][0]
r = A[-1][-1]
while l<r:
m = l + (r - l) // 2
total = 0
for row in A:
total += upper_bound(row, m)
if total >= K:
r = m
else:
l = m + 1
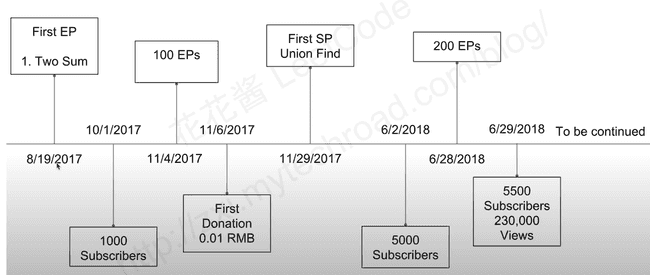
return lSP6: 200 期总结和展望
- Keep track of the latest problems
- Focus on medium / hard problem
- Easy ones can be found on blog
- Publich question only
- new categories
- Comments on Youtube
- Contact me: [email protected]
SP7: Amortized Analysis 均摊分析
Time complexity
- A given algorightm on different inputs of the same size
- Best
- Average
- Worst
- of ops is always the same for the same input
Amortized Analysis
- a sequence of operations on a data structure
- some can be fast
- some can be slow
- What’s the “average” cost over n operations
Array Sorting Algorithms
source: https://www.bigocheatsheet.com/
| Algorithms | Time Complexity | Space Complexity | ||
|---|---|---|---|---|
| Best | Average | Worst | Worst | |
| Quicksort | Ω(n log(n)) | Θ(n log(n)) | O(n^2) | O(log(n)) |
| Mergesort | Ω(n log(n)) | Θ(n log(n)) | O(n log(n)) | O(n) |
| Timsort | Ω(n) | Θ(n log(n)) | O(n log(n)) | O(n) |
| Heapsort | Ω(n log(n)) | Θ(n log(n)) | O(n log(n)) | O(1) |
| Bubble Sort | Ω(n) | Θ(n^2) | O(n^2) | O(1) |
| Insertion Sort | Ω(n) | Θ(n^2) | O(n^2) | O(1) |
| Selection Sort | Ω(n^2) | Θ(n^2) | O(n^2) | O(1) |
| Tree Sort | Ω(n log(n)) | Θ(n log(n)) | O(n^2) | O(n) |
| Shell Sort | Ω(n log(n)) | Θ(n(log(n))^2) | O(n(log(n))^2) | O(1) |
| Bucket Sort | Ω(n+k) | Θ(n+k) | O(n^2) | O(n) |
| Radix Sort | Ω(nk) | Θ(nk) | O(nk) | O(n+k) |
| Counting Sort | Ω(n+k) | Θ(n+k) | O(n+k) | O(k) |
| Cubesort | Ω(n) | Θ(n log(n)) | O(n log(n)) | O(n) |
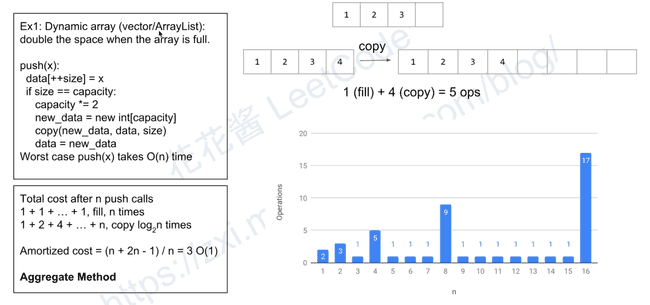
Ex1: Dynamic array(vector/ArrayList):
double the space when the array is full.
Total cost after n push calls
1 + 1 + … + 1, fill n times
1+ 2 + 4 + … + n, copy log2^n times
push(x):
data[++size] = x
if size == capacity:
capacity *= 2
new_data = data int[capacity]
copy(new_data, data, size)
data = new_data
Worst case push(x) takes O(n) timeEx2: Monotonic stack(LC. 901)
When a new element is greater than the top, the top will be poped
Best case: O(1)
[5,4,3,2] push(1), [5,4,3,2,1]
Worst case: O(n)
[5,4,3,2], push(6), [5,4,3,2,6] → [6]
Accounting Method
Credit:
Push: 2 (one for push, one for future pop)
Pop: 0
Charge:
Push: 1, Pop: 1
Your balance is always ≥ 0
Thus the amortized cost is 2.
Aggregate Method
Total cost after n push calls
n elements are pushed on the stack
at most n-1 element can be popped.
Amortized cost ≤ (n+n-1)/n =2O(1)
| op | stack | balance |
|---|---|---|
| - | {} | 0 |
| push(5) | {5} | 1 |
| push(4) | {5,4} | 2 |
| push(3) | {5,4,3} | 3 |
| push(2) | {5,4,3,2} | 4 |
| push(6) | {5,4,3,2} |
{5,4,3} {5,4} {5} {} {6} | 6 5 4 3 2 1 |
SP8 DP1:
- What is DP?
- When to use DP?
- When recursion alone O(2^n) won’t work
- Counting
- Optimization
- Difference between DP and recursion with memorization
What is Dynamic Programming(DP)?
According Wikipedia: DP is a programming method.
Requirements:
- optimal substructure
- “can be solved optimally by breadking it into sub-problems and then recursively finding the optimal solutions to the sub-problems”
- overlapping sub-problems
- sub-problems are overlapped such that we can compute only once and store the solution for future use
- reduce time complexity(Exponential to polynomail)
- if sub-problems do not overlap → divide and conquer
- No-after effect
- the optimal solution of a subproblem will not change when it was used to solve a bigger problem optimally
Top-down:
- recursion with memoization
Bottom-up
- DP
Algorithms that use DP:
- Fibonacci sequence
- LCS
- Knapsack
- Floyd-Warshall
- Bellman-Ford
LC70. Climbing Stairs
Recursion formula:
f(n) = f(n-1) + f(n-2)
f(1) = 1, f(0) = 1
# O(2^n) O(n)
def f(n):
if n<=1: return 1
return f(n-1) + f(n-2)
# O(n), O(n)
def f(n):
if n<=1: return 1
if n not in mem:
mem[n] = f(n-1) + f(n-2)
return mem[n]
f(4) -> f(3) -> f(2) -> f(1)
-> f(0)
-> f(1)
f(2) -> f(1)
-> f(0)
Recursion has redundant computations
O(n), O(n)
def f(n):
dp = [1] * (n + 1)
for i in range(2, n+1):
dp[i] = dp[i-1] + dp[i+2]
return dp[n]
# O(n), O(1)
# One param, no loop
def f(n):
dp1, dp2 = 1, 1
for i in range(2, n+1):
dp2, dp1 = dp1+dp2, dp2
return dp2LC62. Unique Paths
Recursion formula: 2D, Counting
f(x, y) = f(x-1, y) + f(x, y-1)
f(0, 0) = 1, out of board =0
DP: paddings required to handle out of board cases. Actual indies start from 1 instead of 0
#O(mn), O(mn)
def f(x, y):
if x<=0 or y<=0: return 0
if x==1 or y==1: return 1
return f(x-1, y) + f(x, y-1)
#O(mn), O(mn)
def f(x, y):
if x<=0 or y<=0: return 0
if x==1 and y==1: return 1
if (x,y) not in mem:
mem[(x,y)] = f(x-1,y) + f(x,y-1)
return mem[(x,y)]
def f(x,y):
dp = [[0] * (m+1) for _ in range(n+1)]
dp[1][1] = 1
for i in range(1, y+1):
for j in range(1, x+1):
dp[i][j] = dp[i-1][j] + dp[j][i-1]
return dp[y][x]
Galleries: 1D, 2 sets of sub-problems
# LC 926 Flip String to Monotone Increasing
for (int i = 1;i < n; ++i):
l[i] = l[i-1] + S[i] - '0';
for (int i = n -2; i>=0; --i)
r[i] = r[i+1] + '1' - S['i'];
int ans = r[0];
for (int i = 1; i<=n;++i)
ans = min(ans, l[i-1] + r[i]);
LC 845. Longest Mountain in Array
for (int i = 1; i < A.size(); ++i)
if (A[i] > A[i-1]) inc[i] = inc[i-1] + 1;
for (int i = A.size() -2; i>0; --i)
if (A[i] > A[i+1) dec[i] = dec[i+1] + 1;
for ( int i =0; i< A.size(); ++i)
if (inc[i] && dec[i])
ans = max(ans, inc[i] + dec[i] + 1);Galleries: 1D w/ multiple states / dp[i][0], dp[i][i], dp[i][2]…, i is the problem size
# LC 801. Minimun Swaps To Make Sequences Increasing
for i in range(1, n):
if A[i] > A[i-1] and B[i] > B[i-1]:
dp[i][0] = dp[i-1][0]
dp[i][1] = dp[i-1][1] + 1
if B[i] > A[i-1] and A[i] > B[i-1]:
dp[i][0] = min(dp[i][0], dp[i-1][1])
dp[i][1] = min(dp[i][1], dp[i-1][0] + 1)LC 926. Flip String to Monotone Increasing
for i in range(1, n+1):
if S[i-1] == '0':
dp[i][0] = dp[i-1][0]
dp[i][1] = min(dp[i-1][0], dp[i-1][1] + 1
else:
dp[i][0] = dp[i-1][0] + 1
dp[i][1] = min(dp[i-1][0] + dp[i-1][1])LC 790. Domino and Tromino Tilling
for i in range(2, n+1):
dp[i][0] = (dp[i-1][0] + dp[i-2][0]
+ 2 * dp[i-1][1] % kMod)
dp[i][1] = (dp[i-2][0] + dp[i-1][1]) % kModLC 818. Race car
for i in range(1, t+1):
c = min(dp[i][0] + 2, dp[i][1] + 1)
dp[t][0] = min(dp[t][0], dp[t-1][0] + c)
dp[t][1] = min(dp[t][1], dp[t-1][0] + c)Templates
DP
dp = … # create dp array
# add padding if needed
dp[0][0] = … # init dp array
# base cases
for i ...
for j ...
...
dp[i][j] = ... # transition
return dp[n][m]Recursion with memorization
mem = ... # create mem dict
def dp(i, j, ...):
if base_case(i, j): return ... # base cases
if (i, j) not in mem:
mem[(i, j)] = ... # transition
return mem[(i, j)]
return dp(n, m)SP9 DP2:
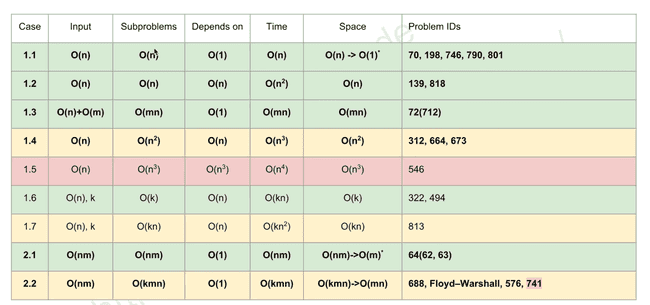
| Case | Input | Subproblems | Depends on | Time | Space | Problems IDs |
|---|---|---|---|---|---|---|
| 1.1 | O(n) | O(n) | O(1) | O(n) | O(n) → O(1) | 70 198 746 790 801 |
| 1.2 | O(n) | O(n) | O(n) | O(n^2) | O(n) | 139 818 |
| 1.3 | O(n)+O(m) | O(mn) | O(1) | O(mn) | O(mn) | 72(7127) |
| 1.4 | O(n) | O(n^2) | O(n) | O(n^3) | O(n^2) | 312 664 673 |
| 1.5 | O(n) | O(n^3) | O(n^3) | O(n^4) | O(n^3) | 546 |
| 1.6 | O(n), k | O(k) | O(n) | O(kn) | O(k) | 322 494 |
| 1.7 | O(n), k | O(kn) | O(n) | O(kn^2) | O(kn) | 813 |
| 2.1 | O(nm) | O(nm) | O(1) | O(nm) | O(nm) →O(m) | 64(62 63) |
| 2.2 | O(nm) | O(knm) | O(1) | O(knm) | O(kmn) → O(mn) | 688, Floyd-Warshall 576 741 |
Category1.1
dp[i] 只依赖比它小的常数项的问题
Input: O(n)
Sub-problems: O(n)
Each sub-problem depends on O(1) smaller problems
Time complexity: O(n)
Space complexity: O(n) -> O(1)
dp[i] := solution of A[1->i] // prefixTemplate
dp = new int[n + 1]
for i = 1 to n:
dp[i] = f(A[i], dp[i-1], dp[i-2], ...)
return dp[n]Problem IDS
70 198 746 790 801
Category1.2
dp[i] 依赖 所有比它小的子问题
Template
dp = new int[n]
for i = 1 to n:
for j = 1 to l-1:
dp[i] = max/min(dp[i], f(dp[j]))
return d[n]Problem ID
139 818
Category1.3
输入是两个 array 或者是两个 string,
dp[i][j] 一般依赖三个(dp[i-1][j] dp[i][j-1] dp[i-1][j-1])
Template
dp = new int[n]
for i = 1 to n:
for j = 1 to l-1:
dp[i] = max/min(dp[i], f(dp[j]))
return d[n]Problem ID
139 818
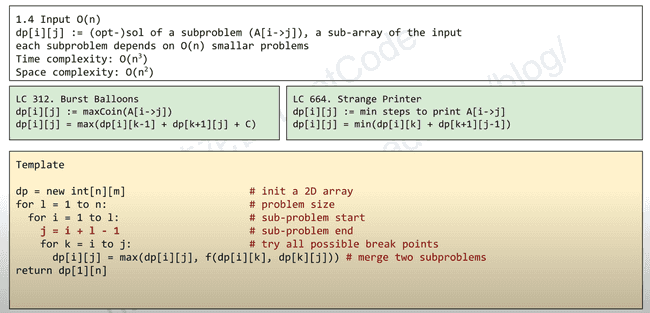
Category1.4
dp[i][j] 依赖 A[i→j]的子数组的解,A[i→j]又依赖 O(n)个子问题。
Template
dp = new int[n]
for i = 1 to n:
for j = 1 to l-1:
dp[i] = max/min(dp[i], f(dp[j]))
return d[n]Problem ID
139 818
Category2.1
dp[i][j] 是子矩阵的解
Template
dp = new int[n]
for i = 1 to n:
for j = 1 to l-1:
dp[i] = max/min(dp[i], f(dp[j]))
return d[n]Problem ID
139 818
Category2.2
dp[k][i][j] = 子矩阵的解在 K 步之后的结果,可降维
k 一般是步数,
Template
dp = new int[K][n][m]
for k = 1 to K:
for i = 1 to n:
for j = 1 to m:
dp[k][i][j] = f(dp[k-1][i+di][j+dj])
return dp[K][n][m] / g(dp[K])Problem ID
139 818
子问题在常数项,可以降维
SP10 0-1 Knapscsk(NP-Complete):
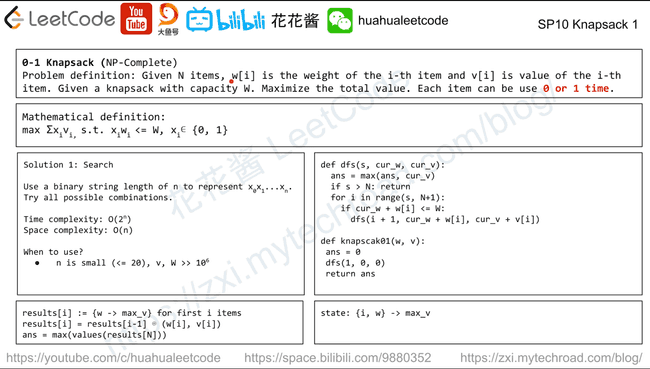
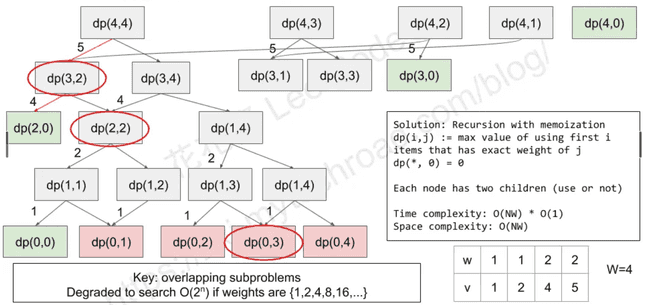
0-1 Knapsack (NP-Complete)
Problem definition: Given N Items, w[i] is the weight of the i-th item and v[i] is value of the i-th item. Given a knapsack with capacity W. Maximize the total value. Each item can be use 0 or 1 time.
Mathematical defintion:
max ZXiVi, s.t.XiWi: <= W, X E {0,1}
Solution 1: Search
Use a binary string length of n to represent X0X1…Xn.
Try all possible combinations.
Time complexity: O(2^n)
Space complexity: O(n)
When to use?
n is small (≤ 20), v, W >> 10^6
def dfs(s, cur_w, cur_v):
ans = max(ans, cur_v)
if s > N: return
for i in range(s, N+1):
if cur_w + w[i] <= W:
dfs(i+1, cur_w + w[i], cur_v + v[i])
def knapscake01(w, v):
ans = 0
dfs(1, 0, 0)
return ansSolution2 : search DFS
def knapsack01DFS(w, v, W):
def dfs(s, cur_w, cur_v, ans):
ans[0] = max(ans[0], cur_v)
if s == N: return
for i in range(s, N):
if cur_w + w[i] <= W:
dfs(i + 1, cur_w + w[i], cur_v + v[i], ans)
ans = [0]
dfs(0, 0, 0, ans)
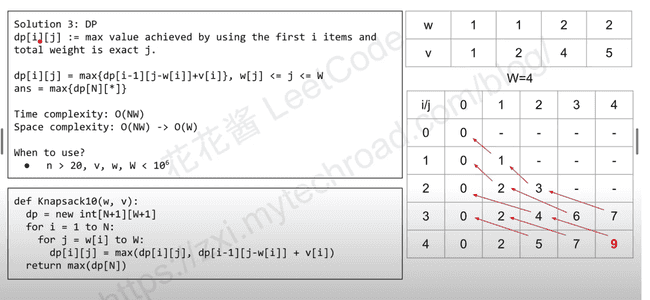
return ans[0]Solution 3 : DP
def knapsack01(w, v, W):
dp = [[0] * (W + 1) for _ in range(N+1)]
for i in range(1, N + 1):
# dp[i] = dp[i-1].clone()
for j in range(1, W + 1):
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i - 1]] + v[i - 1])
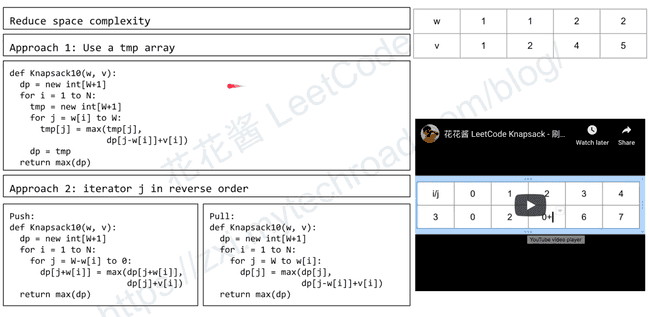
return max(dp[N])Reduce space complexity
Approach 1: dp with tmp array
# dp pull
def knapsack01R(w, v, W):
dp = [0] * (W + 1)
for i in range(0, N):
tmp = list(dp)
for j in range(w[i], W + 1):
tmp[j] = max(tmp[j], dp[j - w[i]] + v[i])
dp = tmp
return max(dp)Approach 2 : iterator j in reverse order
# dp push
def knapsack01R(w, v, W):
dp = [0] * (W + 1)
for i in range(0, N):
tmp = list(dp)
for j in range(w[i], W + 1):
tmp[j] = max(tmp[j], dp[j - w[i]] + v[i])
dp = tmp
return max(dp)# dp pull
def knapsack01R1(w, v, W):
dp = [0] * (W + 1)
for i in range(0, N):
for j in range(W - w[i], -1, -1):
dp[j + w[i]] = max(dp[j + w[i]], dp[j] + v[i])
return max(dp)SP11: Knapsack 2
0-1 Knapsack Problem
Problem definition: Given N items, w[i] is the weight of the i-th item and v[i] is value of the i-th item. Given a knapsack with capacity W. Maximize the total value. Each item can be used 0 or 1 time.
dp[i][j] := max value of using first i items and total weight is exact j.
dp[i][j] = max(dp[i-1][j], # i-th item not used
dp[i-1][j-w[i]]+v[i]) # i-th item usedAns = max(dp[N][*])
Time complexity: O(NW)
Space complexity: O(NW) → O(W)
for i = 1 to N:
for j = 0 to W:
dp[i][j] = max(dp[i-1][j],
dp[i-1][j-w[i] + v[i])
return max(dp[N])Space complexity reduction: Iterate j in reverse order to prevent using i-th item multiple times.
def knapsack01(w, v):
for j = W to w:
dp[j] = max(dp[j], dp[j-w] + v)
for i = 1 to N:
knapsack01(w[i], v[i])
return max(dp[N]Unbounded Knapsack Problem
Problem definition: Given N items, w[i] is the weight of the i-th item and v[i] is value of the i-th item.
Given a knapsack with capacity W. Maximize the total value. Each item can be used 0,1,2,….,times.
Solutio 1: Reduct to 0-1 Knapsack problem (Naive)
Expand the item list, each item appears W/w[i] times.
Time complexity: O(E(W/w[i])*W) = O(W^2)
Space complexity: O(E(W/w[i])*W) = O(W)
def main():
for i = 1 to N:
for j = 1 to W/w[i]:
knapsack01(w[i], v[i])Solutio 2: Reduce to 0-1 Knapsack problem (Smarter?)
Assuming in the optimal sol, item i was used m items, m is a combination of (0, 1, 2, 4, …, 2^k).
Expand the item list:
(w[i], v[i]) → {(w[i], v[i]), (2w[i], 2v[i]),(4w[i], 4v[i]), … , (2^kw[i], 2^kv[i])}, 2^k*w[i] < W
Time complexity: O(Elog(W/w[i])*W) = O(WlogW)
Space complexity: O(Elog(W/w[i])*W) = O(W)
def main():
for i = 1 to N:
for k = 1 to log(W/w[i]):
knapsack01(w[i] << k, v[i] << k)Solutio 3: Use each item more than once more efficiently.
Iterate j in normal order, that’s it.
Time complexity: O(NW)
Space complexity: O(NW) → O(W)
def knapsackUnbounded(w, w):
for j = w to W:
dp[j] = max(dp[j], dp[j-w] + v)
for i = 1 to N:
knapsackUnbounded(w[i], v[i])
return max(dp)Bounded Knapsack Problem
Problem definition: Given N items, w[i]
SP12: Binary Tree
- Definition of a Binary Tree node
- Binary search Tree
- Balanced binary tree
- Binary tree traversal
- Pre-order / In-order / Post-order
- How to create a BST
- Key to tree probelms: recursion
- Templates! Templates! Templates!
- Single root / Two roots
- Time complexity: O(n)
- Space complexity: O(h)
Definition of a Binary Tree node
public class TreeNode{
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) {val = x;}
}
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = Nonestruct TreeNode{
int val;
TreeNode* left = nullptr;
TreeNode* right = nullptr;
TreeNode(int x): val(x) {}
~TreeNode(){
delete left;
delete right;
left = nullptr;
right = nullptr;
}
};
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
delete root;
To create a tree
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.left.right = TreeNode(5)
root.right.left = TreeNode(6)
1
/ \
2 3
/ /
4 6
\
5
Binary search Tree
Binary search tree: vals of left-subtree ≤ root.val < vals of right-subtree
Binary search is not required to be balanced. (correct but might not be efficient)
GOOD
5
/
4
/
3
/
2
/
1 GOOD
5
/ \
3 7
/ /
1 6BAD
5
/ \
3 7
/ /
1 4func search(root, x):
if not root: return False
if x == root.val: return True
if x < root.val:
return search(root.left, x)
else:
return search(root.right, x)
Time complexity: O(h)
Worst case: O(h) = O(n)
Best case: O(h) = O(logn)Balanced Tree:
The height of left/right subtrees are at most 1.
def balanced(root):
if not root: return True
return abs(height(root.left) - height(root.right)) <= 1
and balanced(root.left) and balanced(root.right)
def height(root):
if not root: return 0
left = height(root.left)
right = height(root.right)
return max(left, right) + 1 5
/
4
/
3
/
2
/
1
A BST but not balanced inefficient 5
/ \
4 7
/ \ /
2 3 4
/
1
A balanced tree but not a BST
Not useful at all 5
/ \
3 7
/ \ /
1 4 6
A perfect BST
O(h) = O(logn)
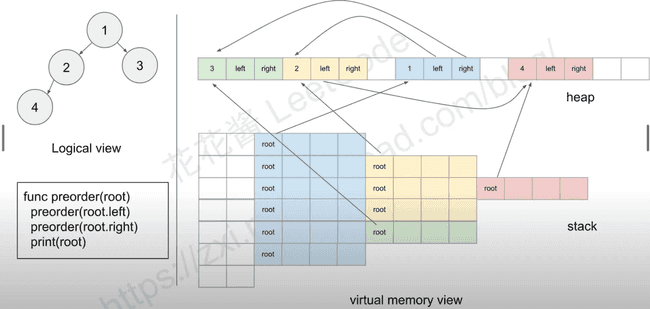
Tree Traversal
def perorder(root):
if not root: return
print(root.val)
perorder(root.left)
perorder(root.right)
# [5, 3, 1, 4, 7, 6]def inorder(root):
if not root: return
inorder(root.left)
print(root.val)
inorder(root.right)
# [1, 3, 4, 5, 6, 7]
# For a BST the vals are sorted!def postorder(root):
if not root: return
postorder(root.left)
postorder(root.right)
print(root.val)
# [1, 4, 3, 6, 7, 5]How to create a (unbalanced) BST
insert returns the new root of the subtree
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
def createBST(nums):
root = None
for num in nums:
root = insert(root, num)
return root
def insert(root, val):
if not root:
return TreeNode(val)
if val <= root.val:
root.left = insert(root.left, val)
else:
root.right = insert(root.right, val)
return root
def inorder(root, v):
if not root:
return
inorder(root.left, v)
v.append(root.val)
inorder(root.right, v)
if __name__ == '__main__':
root = createBST([5, 3, 1, 4, 7, 6])
v = []
inorder(root, v)
print(v)
// insert returns the new root of the subkey to solve tree problems: Thinking in a recursive way.
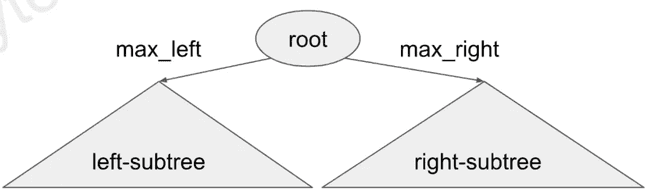
Example: find the max val of tree
# Traditional way:
ans = -inf
def maxVal(root):
ans = -inf
traverse(root)
return ans
def traverse(root):
if not root: return
ans = max(ans, root.val)
traverse(root.left)
traverse(root.right)# Recursive way:
def maxVal(root):
if not root: return -inf
max_left = maxVal(root.left)
max_right = maxVal(root.right)
return max(max_left, max_right)Template 1: one root
def solve(root):
if not root: return ...
if f(root): return ...
l = solve(root.left)
r = solve(root.rigth)
return g(root, l, r)# LC 104. Maximum Depth of Binary Tree.
def maxDepth(root):
if not root: return 0
l = maxDepth(root.left)
r = maxDepth(root.right)
return max(l, r) + 1# LC 111. Minium Depth of Binary Tree
def minDepth(root):
if not root: return 0
if not root.left and not root.right: return 1
l = minDepth(root.left)
r = minDepth(root.right)
if not root.left: return 1 + r
if not root.right: return 1 + l
return min(l, r) + 1# LC 112. Path Sum.
def pathSum(root, sum):
if not root: return false
if not roo.left and not root.right: return root.val == sum
l = pathSum(root.left, sum - root.val)
r = pathSum(root.right, sum - root.right)
return l or rTemplate 2: two root
def solve(p, q):
if not p and not q: return ...
if f(p, q): return ...
c1 = solve(p.child, q.child)
c2 = solve(p.child, q.child)
return g(p, q, c1, c2)# LC 100. Same Tree
def sameTree(p, q):
if not p and not q: return True
if not p or not q: return False
l = sameTree(p.left, q.left)
r = sameTree(p.right, q.right)
return p.val == q.val and l and r# LC 101. Symmetric Tree
def sameTree(p, q):
if not p and not q: return True
if not p or not q: return False
l = sameTree(p.left, q.right)
r = sameTree(p.right, q.left)
return p.val == q.val and l and r# LC 951. Flip Equivalent Binary Trees
def flipEquiv(p, q):
if not p and not q: return True
if not p or not q: return False
l1 = flipEquiv(p.left, q.left)
l2 = flipEquiv(p.left, q.right)
r1 = flipEquiv(p.right, q.right)
r2 = flipEquiv(p.left, q.right)
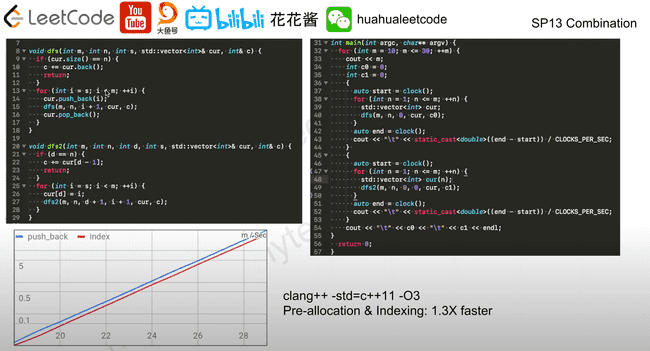
return p.val == q.val and ((l1 and r1) or (l2 and r2))SP13: Combination
Combination:
nums = […]
ans = []
m = len(nums)
# C(m, n)
def dfs(n, s, cur):
if len(cur) == n:
ans.append(cur[:])
return
for i in range(s, m):
cur.append(nums[i])
dfs(n, i+1, cur)
cur.pop()
for i in range(0, m+1):
dfs(i, 0, [])
n=0
ans.append(cur)n=1
for i in range(0, m):
cur.append(nums[i]
ans.append(cur)
cur.pop()n=2
for i in range(0, m):
cur.append(nums[i])
for j in range(i, m):
cur.append(nums[j])
ans.append(cur)
cur.pop()
cur.pop()n=3
for i in range(0, m):
cur.append(nums[i])
for j in range(i+1, m):
cur.append(nums[j])
for k in range(j+1, m):
cur.append(nums[k])
ans.append(cur)
cur.pop()
cur.pop()
cur.pop()n=4
for i in range(0, m):
cur.append(nums[i])
for j in range(i+1, m):
cur.append(nums[j])
for k in range(j+1, m):
cur.append(nums[k])
for l in range(k+1, m):
cur.append(nums[l])
ans.append(cur)
cur.pop()
cur.pop()
cur.pop()
cur.pop()
Combination: with dfs depth
nums = [...]
ans = []
m = len(nums)
# C(m, n)
def dfs(n, d, s, cur):
if d == n:
ans.append(cur[0:d])
return
for i in range(s, m):
cur[d] = nums[i]
dfs(n, d+1, i+1, cur)
~~cur[d] = None~~
for i in range(0, m+1):
dfs(i, 0 [None]*i)n = 0
ans.append(cur)
n = 1
for i range(0, m):
cur[0] = nums[i]
ans.append(cur)
n = 2
for i range(0, m):
cur[0] = nums[i]
for j in range(i+1, m):
cur[1] = nums[j]
ans.append(cur)n = 3
for i range(0, m):
cur[0] = nums[i]
for j in range(i+1, m):
cur[1] = nums[j]
for k in range(j+1, m):
cur[2] = nums[k]
ans.append(cur)
n = 4
for i range(0, m):
cur[0] = nums[i]
for j in range(i+1, m):
cur[1] = nums[j]
for k in range(j+1, m):
cur[2] = nums[k]
for l in range(k+1, m):
cur[3] = nums[l]
ans.append(cur)Permutation
nums = [...]
ans = []
m = len(nums)
used = [False] * m
# P(m, n)
def dfs(n, cur):
if len(cur) == n:
ans.append(cur[:])
return
for i range(0, m):
if used[i]: continue
used[i] = True
cur.append(nums[i])
dfs(n, cur)
cur.pop()
used[i] = False
for i in range(0, len(nums)+1):
dfs(i, [])
n = 0
ans.append(cur)
n = 1
for i in range(0, m):
if used[i]: continue
used[i] = True
cur.append(nums[i])
ans.append(cur)
cur.pop()
used[i] = False
n = 2
for i in range(0, m):
if used[i]: continue
cur.append(nums[i])
for j in range(0, m):
if used[j]: continue
used[j] = True
cur.append(nums[j])
ans.append(cur)
cur.pop()
used[j] = False
cur.pop()
used[i] = Falsen = 3
for i in range(0, m):
if used[i]: continue
used[i] = True
cur.append(nums[i])
for j in range(0, m):
if used[j]: continue
used[j] = True
cur.append(nums[j])
for k in range(0, m):
if used[k]: continue
used[k] = True
cur.append(nums[k])
ans.append(cur)
cur.pop()
usded[k] = False
cur.pop()
used[j] = False
cur.pop()
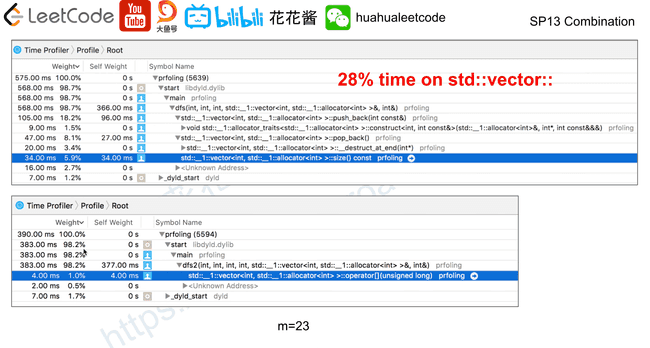
used[i] = FalsePerformance measurement
Benchmarking
- Same set of inputs
- Absolute runing time
- Different version of programs running on the same hardware
- Same version of program running on different hardwares
Profiling
- Relative running time
- Identify the hostpots(usually a few functions)
- One of my program spent ~ 50% on sqrt
- Optimize those hotspots and do benchmarking again
SP14: Segment Tree
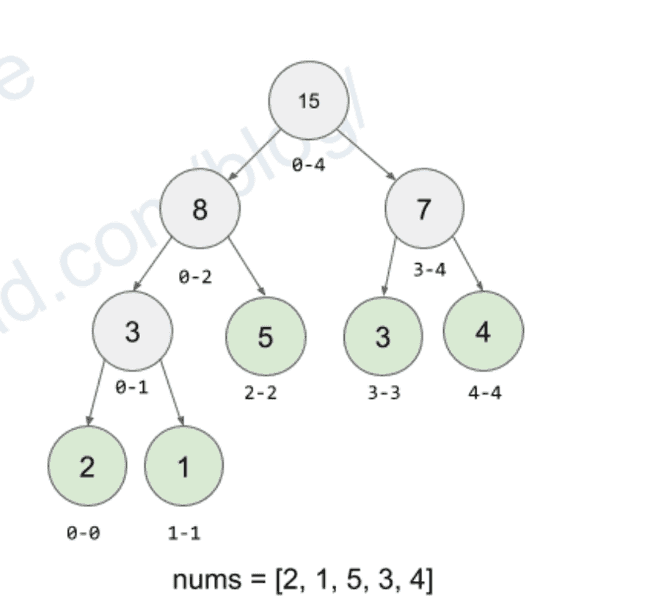
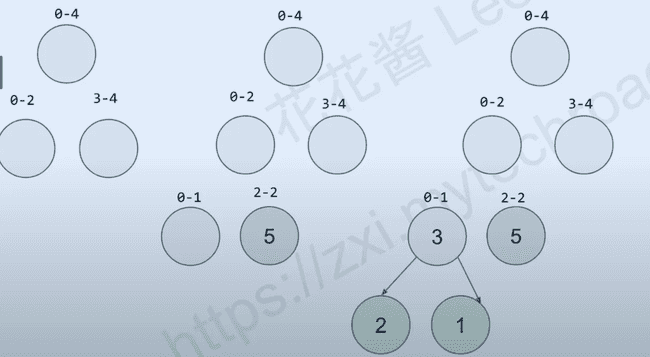
Discrete version of a Segment Tree:
A balanced binary tree. O(logn) height given n elements.
Each leaf node(segment) represents an element in the array. Each non leaf node covers the union of its children’s range.
Operations:
- build(start, end, vals) → O(n)
- update(index, value) → O(logn)
- rangeQuery(start, end) → O(logn + k)
- where k is the number of reported segments
15
[0-4]
/. \
8 7
[0-2] [3-4]
/ \ / \
3 5 3 4
[0-1][2][3] [4]
/ \
2 1
[0] [1]
nums = [2, 1, 5, 3, 4]code
class SegmentTreeNode:
def __init__(self, start, end, sum, left=None, right=None):
self.start = start
self.end = end
self.sum = sum
self.left = left
self.right = right
def buildTree(start, end, vals):
if start == end:
return SegmentTreeNode(start, end, vals[start])
mid = (start + end) // 2 # 使用整除
left = buildTree(start, mid, vals)
right = buildTree(mid+1, end, vals)
return SegmentTreeNode(start, end, left.sum + right.sum, left, right)
def updateTree(root, index, val):
if root.start == root.end == index:
root.sum = val
return
mid = (root.start + root.end) // 2
if index <= mid:
updateTree(root.left, index, val)
else:
updateTree(root.right, index, val)
root.sum = root.left.sum + root.right.sum
# updateTree: Similar to binary search
# T(n) = T(n/2) + O(1) = log(n)
# Don't forget to update root's sum
def querySum(root, i, j):
if root.start == i and root.end == j:
return root.sum
mid = (root.start + root.end) // 2
if j <= mid:
return querySum(root.left, i, j)
elif i > mid:
return querySum(root.right, i, j)
else:
return querySum(root.left, i, mid) + querySum(root.right, mid+1, j)
# QueryTree: O(log(n) + k)
# Ex 1: querySum(n15, 3, 4)[7]
# querySum(n7, 3, 4) <- 7
# Ex 2: querySum(n15, 2, 2)[5]
# querySum(n8, 2, 2][5]
# querySum(n5, 2, 2] <- 5
# Ex 3: querySum(n15, 1, 3)[9]
# querySum(n8, 1, 2)[6] + querySum(n7, 3, 3)[3]
# querySum(n3, 1, 1[1] + querySum(n5, 2, 2) <- 5 querySum(n3, 3, 3) <- 3
# querySum(n1, 1, 1) <- 1
# 测试用例
nums = [2, 1, 5, 3, 4]
root = buildTree(0, len(nums) - 1, nums)
# 验证线段树
def printTree(node):
if node is not None:
print(f"[{node.start}, {node.end}] : {node.sum}")
printTree(node.left)
printTree(node.right)
print("更新前的线段树")
printTree(root)
updateTree(root, 2, 10) # 将索引 2 的值更新为 10
print("更新后的线段树")
printTree(root)
print("查询区间 [1,3] 的和:", querySum(root, 1, 3))
print("查询区间 [0,4] 的和:", querySum(root, 0, 4))
print("查询区间 [2,2] 的和:", querySum(root, 2, 2))307. Range Sum Query - Mutable
class SegmentTreeNode {
public:
SegmentTreeNode(int start, int end, int sum,
SegmentTreeNode* left = nullptr,
SegmentTreeNode* right = nullptr):
start(start),
end(end),
sum(sum),
left(left),
right(right){}
SegmentTreeNode(const SegmentTreeNode&) = delete;
SegmentTreeNode& operator=(const SegmentTreeNode&) = delete;
~SegmentTreeNode() {
delete left;
delete right;
left = right = nullptr;
}
int start;
int end;
int sum;
SegmentTreeNode* left;
SegmentTreeNode* right;
};
class NumArray {
public:
NumArray(vector<int> nums) {
nums_.swap(nums);
if (!nums_.empty())
root_.reset(buildTree(0, nums_.size() - 1));
}
void update(int i, int val) {
updateTree(root_.get(), i, val);
}
int sumRange(int i, int j) {
return sumRange(root_.get(), i, j);
}
private:
vector<int> nums_;
std::unique_ptr<SegmentTreeNode> root_;
SegmentTreeNode* buildTree(int start, int end) {
if (start == end) {
return new SegmentTreeNode(start, end, nums_[start]);
}
int mid = start + (end - start) / 2;
auto left = buildTree(start, mid);
auto right = buildTree(mid + 1, end);
auto node = new SegmentTreeNode(start, end, left->sum + right->sum, left, right);
return node;
}
void updateTree(SegmentTreeNode* root, int i, int val) {
if (root->start == i && root->end == i) {
root->sum = val;
return;
}
int mid = root->start + (root->end - root->start) / 2;
if (i <= mid) {
updateTree(root->left, i, val);
} else {
updateTree(root->right, i, val);
}
root->sum = root->left->sum + root->right->sum;
}
int sumRange(SegmentTreeNode* root, int i, int j) {
if (i == root->start && j == root->end) {
return root->sum;
}
int mid = root->start + (root->end - root->start) / 2;
if (j <= mid) {
return sumRange(root->left, i, j);
} else if (i > mid) {
return sumRange(root->right, i, j);
} else {
return sumRange(root->left, i, mid) + sumRange(root->right, mid + 1, j);
}
}
};SP15: 刷题
每天 2-3 小时,一个月 100 个小时
- LeetCode 在 2 月底就将进入千题时代(ZOJ 笑而不语)
- 要刷多少题?
- 每个类型 10-20 题(动态规划:多多益善)
- 总共 200 - 300 题
- 如何刷题?
- 同类型的题目一起刷。e.g. 周一:树/链表,周二:搜索,周三:动态规划。。。
- 第一遍:5 分钟想不出来就看答案
- 第二遍:尝试不看答案完整实现(一道题不要超过 60 分钟)
- 第三遍:尝试快速实现,如果 15-20 分钟内实现不了就看答案
- 看代码很重要!看代码很重要!看代码很重要!
- 看至少 3-5 种不同的实现,分析别人的代码,优缺点,为什么速度快/慢?
- 学习新的语言/算法/数据结构/API/模版/最佳实践
- 刷题过程中培养的能力
- 扩宽的思路,至少能看出该使用什么样的算法
- 数据规模 → 时间复杂度推算
- 代码风格:1. 一致性:命名/锁进/括号/换行 2. 有意义的变量名
SP16:
[https://docs.google.com/spreadsheets/d/1SbpY-04Cz8EWw3A_LBUmDEXKUMO31DBjfeMoA0dlfIA/edit?gid=1486450114#gid=1486450114](https://docs.google.com/spreadsheets/d/1SbpY-04Cz8EWw3A_LBUmDEXKUMO31DBjfeMoA0dlfIA/preview?gid=1486450114#gid=1486450114)
https://zxi.mytechroad.com/blog/leetcode-problem-categories/
SP17: Binary Search II
Is there any difference between
- [l, r+1)
- [l, r)
- (l-1, r+1)
No difference in terms of output as long as all of them implement:
Given a function g, returns the smalleset m in the given range such that g(m) is True.
The internal representation can be off by 1 or 2, but the output should be exactly the same.
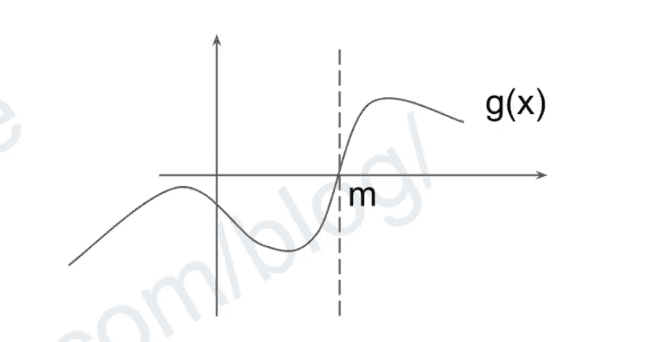
g(x) is a function that
exist m s.t. g(x) > 0 (True) if x≥ m else ≤ 0 (False)
The key to binary search is Don’t trying to find the exact answer, but find a split point m such that for all n, n ≥ m, conditions are satisfied, then m will naturally become the answer for free.
左闭右开 [l, r)
"""
Returns the smallest number m in range [l, r) such
that g(m) is true. Returns r if not found.
"""
def binary_search(l, r):
while l < r:
m = l + (r - l) // 2
if g(m):
r = m
else:
l = m + 1
return l闭区间 [l, r]
"""
Returns the smallest number m in range [l, r] such that g(m) is true.
Returns r if not found.
"""
def binary_search(l, r):
while l <= r:
m = l + (r - l) // 2
if g(m):
r = m - 1
else:
l = m + 1
return l
Search range[10, 101], g(m) = True if m > 25 else False
SP18: Minimum Spanning Tree
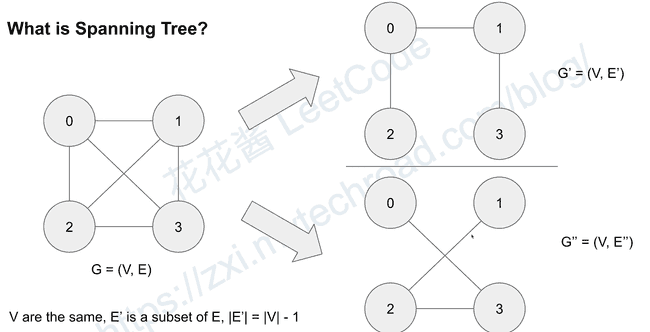
- What is spanning tree?
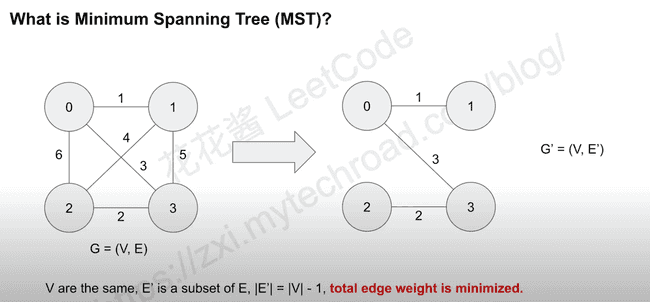
- What is minium spanning tree (MST) ?
- Graph representation
- Adjacency matrix (邻接矩阵)
- Adjacency list (临接表)
- Edge list (边表)
- Algorithms to compute MST
- Prim
- Kruskal
what is Spanning Tree?
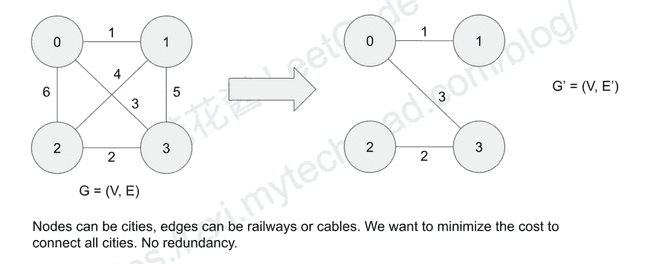
what is Mininum Spanning Tree(MST)?
Why we need MSTs?
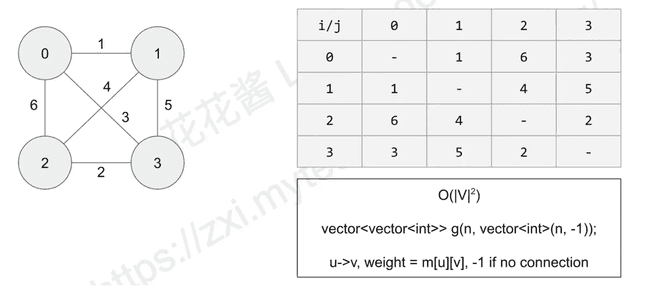
Graph representation: Adjacency matrix
Graph representation: Adjacency list (dynamic array)
Graph representation: Edge list
Algorithms to compute MST
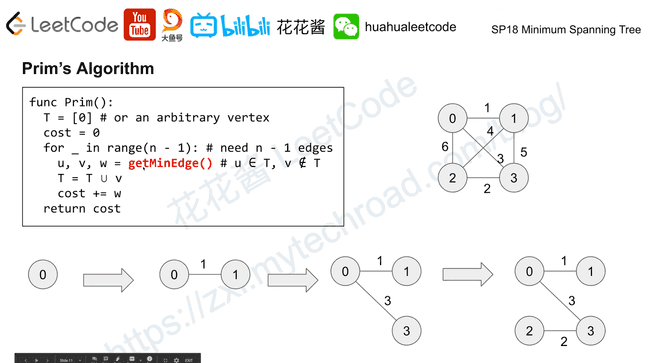
Prim’s Algorithm
- Vojtech Jarnik, 1930
- Robert C. Prim, 1957
- Edsger W.Dijkstra in 1959
A greedy algorithm, building the tree by adding one vertex each step.
| Data structure | Time complexity | | ------------------------------- | --------------- | --- | --- | --- | --- | --- | --- | --- | | Adjacency matrix | O( | V | ^2) | | Binary heap + adjacency list | O( | E | log | V | ) | | Fibonacci heap + adjacency list | O( | E | + | V | | log | V | ) |
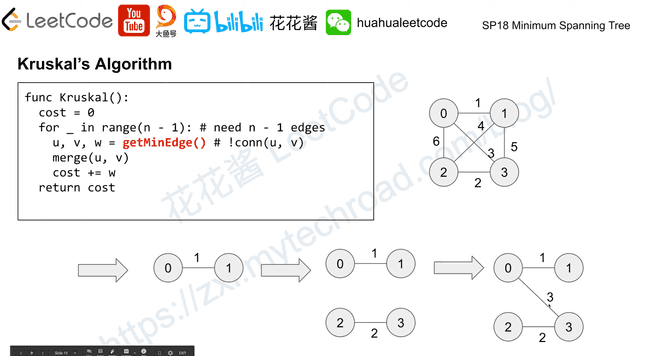
Kruskal’s Algorithm
- Joseph Kruskal, 1956
Also a greedy algorithm, building the tree by mergin minimun spaning forest. (Union-find)
Time complexity: O(|E|log|V|)
Prim’s Algorithm
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
int main(int argc, char** argv) {
const int n = 4;
vector<vector<int>> edges{{0,1,1},{0,3,3},{0,2,6},{2,3,2},{1,2,4},{1,3,5}};
vector<vector<pair<int, int>>> g(n);
for (const auto& e : edges) {
g[e[0]].emplace_back(e[1], e[2]);
g[e[1]].emplace_back(e[0], e[2]);
}
priority_queue<pair<int, int>> q; // (-w, v)
vector<int> seen(n);
q.emplace(0, 0); // (-w, v)
int cost = 0;
for (int i = 0; i < n; ++i) {
while (true) {
const int w = -q.top().first;
const int v = q.top().second;
q.pop();
if (seen[v]++) continue;
cost += w;
for (const auto& p : g[v]) {
if (seen[p.first]) continue;
q.emplace(-p.second, p.first);
}
break;
}
}
cout << cost << endl;
return 0;
}from collections import defaultdict
from heapq import *
n = 4
edges = [[0,1,1],[0,3,3],[0,2,6],[2,3,2],[1,2,4],[1,3,5]]
g = defaultdict(list)
for e in edges:
g[e[0]].append((e[1], e[2]))
g[e[1]].append((e[0], e[2]))
q = []
cost = 0
seen = set()
heappush(q, (0, 0))
for _ in range(n):
while True:
w, u = heappop(q)
if u in seen: continue
cost += w
seen.add(u)
for v, w in g[u]:
if v in seen: continue
heappush(q, (w, v))
break
print(cost)#include <iostream>
#include <queue>
#include <vector>
#include <functional>
#include <numeric>
using namespace std;
int main(int argc, char** argv) {
const int n = 4;
vector<vector<int>> edges{{0,1,1},{0,3,3},{0,2,6},{2,3,2},{1,2,4},{1,3,5}};
vector<vector<int>> q; // (w, u, v)
for (const auto& e : edges)
q.push_back({e[2], e[0], e[1]});
sort(begin(q), end(q));
vector<int> p(n);
iota(begin(p), end(p), 0);
function<int(int)> find = [&](int x) {
return x == p[x] ? x : p[x] = find(p[p[x]]);
};
int cost = 0;
for (const auto& t : q) {
int w = t[0], u = t[1], v = t[2];
int ru = find(u), rv = find(v);
if (ru == rv) continue;
p[ru] = rv; // merge (u, v)
cost += w;
}
cout << cost << endl;
return 0;
}from collections import defaultdict
from heapq import *
n = 4
edges = [[0,1,1],[0,3,3],[0,2,6],[2,3,2],[1,2,4],[1,3,5]]
p = list(range(n)
def find(x):
if x != p[x]:
p[x] = find(p[p[x]]
return p[x]
cost = 0
for u, v, w in sorted(edges, key=lambds x: x[2]):
ru, rv = find(u), find(v)
if ru == rv: continue
p[ru] = rv
cost += w
print(cost)
https://zxi.mytechroad.com/blog/sp/minimum-spanning-tree-sp18/
有向图中的 topological sort 拓扑排序和 critical path 关键路径
LC1135 和 1168 用了 MST
SP19: KMP string-searching-algorithm
-
String searching problem:
- Given a string s and a pattern p, find the all occurrences of p in s.
- e.g.
- match(s=’abcdefgcde’, p=’cde’) → [2, 7]
- match(s=’abcdefgcde’, p=’cba’) → [], not found
-
Navie algorithm (brute force):
-
n = len(s), m = len(p)
-
Try all possible substrings of s with ealry return
-
Worst case: O(n*m)
-
The longest prefix of p occurs O(n) times in s
-
s = ‘aaaaaaaa….aaab’, p = ‘aaab’ aaaa…aaaaab aaab
… aaab
-
-
Average case: O(n+m): For random inputs: P(s[i] == p[j]) == 1/k, the expected matching length is O(1).
-
-
KMP (Knuth-Morris-Pratt)
- Fast Pattern Matching in Strings (SIAM ‘77)
- Guaranteed worst case performace: O(m+n)
- Two stages:
- Pre-processing: table building O(m)
- Matching: O(n)
- Two stages:
- Space complexity: O(m)
def match(s, p):
"""
Args:
s: input string
p: pattern to search
"""
ans = [] # matched indices
nxt = build(p) # build next table
n = len(s)
m = len(p) # added len of pattern to avoid calling len many times
j = 0
for i in range(n): # i, j: pointer of s and p respectively
while j > 0 and s[i] != p[j]:
j = nxt[j] # Accessing the correct nxt index
if s[i] == p[j]: # match then check next pair (i++, j++)
j += 1
if j == m: # found a full match
ans.append(i - m + 1)
j = nxt[j] # jump as it failed
return ans
def build(p):
"""
build the next array for KMP algorithm
"""
m = len(p)
nxt = [0] * m
j = 0
for i in range(1, m):
while j > 0 and p[i] != p[j]:
j = nxt[j-1]
if p[i] == p[j]:
j += 1
nxt[i] = j
return nxt
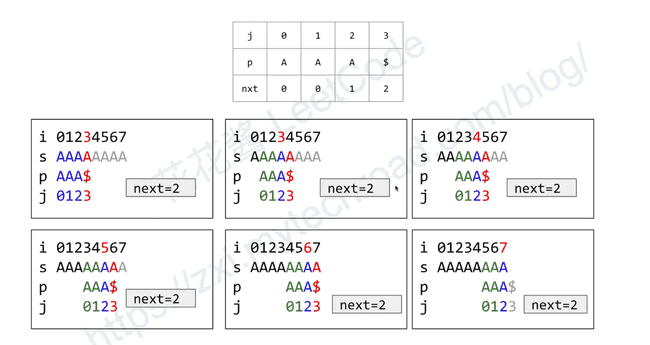
# nxt[i] 表示 p 的前 i+1 个字符(p[0...i])中,最长公共前缀后缀的长度KMP::Match
- Case 1: s[i] == s[j], match
- Action: ++i, ++j: try next pair ABCABCD ⇒ ABCABCD ⇒ ABCABCD ABC… ABC… ABC…
- Case 2: s[i] ≠ p[j], a miamatch happened
- key idea: use partial matching information
- Let q = p[0~j-1] be the partial matched string
- Action: i remains the same, if j == 0: ++i else: j = next[j],
- Case 2.1: q is empty (e.g. j = 0)
- ++i, try next one ABCABCD ABCABCD ABCD ⇒ ABCD
- Case 2.2:
- Case 2.3:
- Case 2.4:
Proof of linear time complexity for Match:
- every ++j comes with a ++i, i never decreases ⇒ j will be increased at most O(n) times.
- nxt[j] < j, j = nxt[j], j becomes smaller, j can be decreased at most O(n) times.
At most O(2n) operations on j ⇒ Time complexity: O(n)
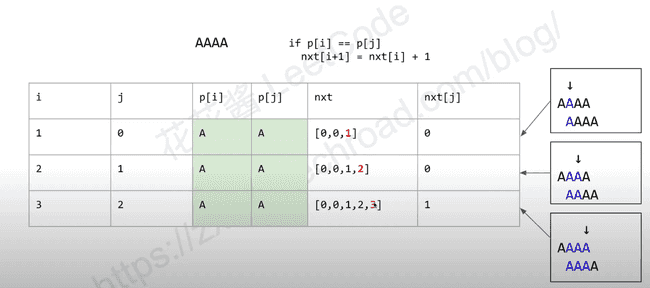
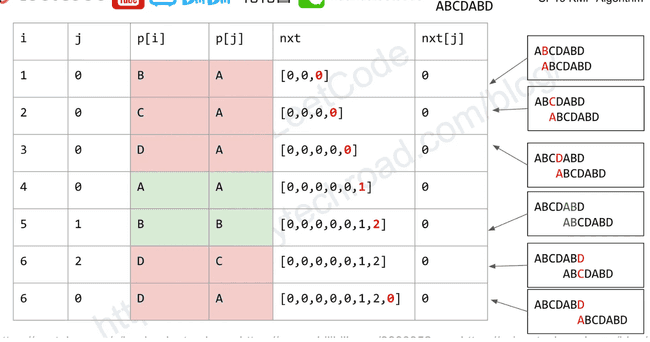
Build: Next table / Partial match table / failure function
next[i] := len of the longest prefix of p[0:i] that is also the suffix len(next) = len(p) + 1
Time complexity: O(m)
def build(p):
"""
build the next array for KMP algorithm
Args:
p: pattern to build
"""
m = len(p)
nxt = [0, 0]
j = 0
for i in range(1, m):
while j > 0 and p[i] != p[j]:
j = nxt[j]
if p[i] == p[j]:
j += 1
nxt.append(j)
return nxtfrom typing import List
def build(p: str) -> List[int]:
m = len(p)
nxt = [0, 0]
j = 0
for i in range(1, m):
while j > 0 and p[i] != p[j]:
j = nxt[j]
if p[i] == p[j]:
j += 1
nxt.append(j)
return nxt
def match(s: str, p: str) -> List[int]:
n, m = len(s), len(p)
nxt = build(p)
j = 0
ans = []
for i in range(n):
while j > 0 and s[i] != p[j]:
j = nxt[j]
if s[i] == p[j]:
j += 1
if j == m:
ans.append(i - m + 1)
j = nxt[j]
return ans
def checkeq(actual, expected):
if actual != expected:
print("actual: %s, expected: %s" % (actual, expected))
else:
print("Pass")
if __name__ == "__main__":
checkeq(build("abcdabd"), [0, 0, 0, 0, 0, 1, 2, 0])
checkeq(build("ab"), [0, 0, 0])
checkeq(build("a"), [0, 0])
checkeq(build("aa"), [0, 0, 1])
checkeq(build("aaaa"), [0, 0, 1, 2, 3])
checkeq(build("aaba"), [0, 0, 1, 0, 1])
checkeq(match("ABC ABCDAB ABCDABCDABDE", "ABCDABD"), [15])
checkeq(match("ABC ABCDAB ABCDABCDABDE", "AB"), [0, 4, 8, 11, 15, 19])
checkeq(match("ABC ABCDAB ABCDABCDABDE", "B"), [1, 5, 9, 12, 16, 20])
checkeq(match("AAAAA", "A"), [0, 1, 2, 3, 4])
checkeq(match("AAAAA", "AA"), [0, 1, 2, 3])
checkeq(match("AAAAA", "AAAA"), [0, 1])
checkeq(match("AAAAA", "AAAAA"), [0])
checkeq(match("AABAABA", "AAB"), [0, 3])Example:
LeetCode: 28. Implement strStr()
class Solution{
public:
int strStr(string haystack, string needle){
if (needle.empty()) return 0;
auto matches = KMP::Match(haystack, needle);
return matches.empty() ? -1 : matches[0];
}
}LeetCode: 459. Repeated Substring Pattern
class Solution{
public:
bool repeatedSubstringPattern(string str){
const int n = str.length();
auto nxt = KMP::Build(str);
return nxt[n] && n % (n - nxt[n]) == 0;
}
}LeetCode 1392. Longest Happy Prefix
#include <iostream>
#include <string>
#include <vector>
using namespace std;
class KMP {
public:
static vector<int> Build(const string& s) {
int n = s.size();
std::vector<int> pi(n, 0);
for (int i = 1; i < n; ++i) {
int j = pi[i - 1];
while (j > 0 && s[i] != s[j]) {
j = pi[j - 1];
}
if (s[i] == s[j]) {
++j;
}
pi[i] = j;
}
return pi;
}
};
class Solution {
public:
string longestPrefix(const string& s){
return s.substr(0, KMP::Build(s).back());
}
};
int main() {
Solution solution;
string s1 = "abab";
string s2 = "leetcodeleet";
string s3 = "a";
string s4 = "aaaaa";
string s5 = "ababab";
cout << solution.longestPrefix(s1) << endl; // Output: aba
cout << solution.longestPrefix(s2) << endl; // Output: leet
cout << solution.longestPrefix(s3) << endl; // Output: a
cout << solution.longestPrefix(s4) << endl; // Output: aaaaa
cout << solution.longestPrefix(s5) << endl; // Output: ababa
return 0;
}SP20: Fast Power of DP
DP 优化求极值/组合计数求某种特定方法的数量 → 快速幂
LeetCode 1411. Number of Ways to Paint N * 3 Grid
dp[i][0] = 3 * dp[i-1][0] + 2*dp[i-1][1]
dp[i][1] = 2 * dp[i-1][0] + 2*dp[i-1][1]
dp[1][0] = 6, dp[1][1] = 6, Find dp[n][0] + dp[n][1]
Naive for loop takes O(n) Time? Can we do better ? Yes!
We can rewrite in matrix multiplication form:
|dp[n][0] dp[n][1]| = | dp[n-1][0] dp[n-1][1] * | 3 2 |
| 2 2 |
= | dp[0][0]=6, dp[0][1]=6 | * | 3 2 | ^ ( n - 1 )
| 2 2 |Q: How to compute the power of a matrix (or a number) fast ?
Fast Power by Squaring
x = a * b^n, n is integers and n ≥ 1, a, b canbe integers or matrices
Binary representation of n:
x = 2 _ 3^43 = 2 _ 3^(1+2+8+32) = 2 _ 3 _ 3^2 _ 3^8 _ 3 ^32
def power(a, b, n): # Time complexity: O(logn)
x = a
while n > 0:
if n & 1 == 1: # current bit is 1
x *= b # x = mul(x, b) for matrices
b *= b # b = mul(b, b) for matrices
n >>= 1
return x| x | b | n |
|---|---|---|
| 2 | 3 | 43 |
| 2*3 | 3^2 | 21 |
| 2*3^3 | 3^4 | 10 |
| 2*3^3 | 3^8 | 5 |
| 2*3^11 | 3^16 | 2 |
| 2*3^11 | 3^32 | 1 |
| 2*3^43 | 3^64 | 0 |
LeetCode 1411. Number of Ways to Paint N x 3 Grid
| dp[n][0] dp[n][1] | = |dp[0][0]=6 dp[0][1]=6 | * | 3 2 | ^ ( n - 1)
| 2 2|class Solution{
public:
int numOfWays(int n){
constexpr long kMod = 1e9 + 7;
auto mul = [kMod](const vector<vector<long>>& A,
const vector<vector<long>>& B){
const int m = A.size();
const int n = N.size();
const int p = B[0].size();
vector<vector<logn>> C(m, vector<long>(p));
for (int i=0; i< m; ++i)
for (int j =0; j<p; ++j)
for(int k = 0; k < n; ++k)
C[i][j] = (C[i][j] + A[i][k] * B[k][j]) % kMod;
return C;
};
vector<vector<long>> ans{{6,6}}; // 1x2
vector<vector<long>> M{{3, 2}, {2, 2}}; // 2*2
--n;
while(n){
if (n&1) ans = mul(ans, M); // ans = ans * M;
M = mul(M, M); // M = M^2
n >>= 1;
}
// ans = ans0 * M^(n-1)
return (ans[0][0] + ans[0][1]) % kMod;
}
};
935. Knight Dialer
class Solution {
public:
int knightDialer(int N){
constexpr long kMod = 1e9 + 7;
auto mul = [kMod](const vector<vector<long>>& A,
const vector<vector<long>>& B) {
const int m = A.size();
const int n = B.size();
const int p = B[0].size();
vector<vector<long>> C(m, vector<long>(p));
for ( int i = 0; i < m; ++i)
for ( int j = 0; j < p; ++j)
for ( int k = 0; k < n; ++k)
C[i][j] = (C[i][j] + A[i][k] * B[k][j]) % kMod;
return C;
};
vector<vector<long>> ans(1, vector<long>(10, 1));
vector<vector<long>> M{
{0,0,0,0,1,0,1,0,0,0}, // 0 -> 4, 6
{0,0,0,0,0,0,1,0,1,0}, // 1 -> 6, 8
{0,0,0,0,0,0,0,1,0,1}, // 2 -> 7, 9
{0,0,0,0,1,0,0,0,1,0}, // 3 -> 4, 8
{1,0,0,1,0,0,0,0,0,1}, // 4 -> 0, 3, 9
{0,0,0,0,0,0,0,0,0,0}, // 5 -> None
{1,1,0,0,0,0,0,1,0,0}, // 6 -> 0, 1, 7
{0,0,1,0,0,0,1,0,0,0}, // 7 -> 2, 6
{0,1,0,1,0,0,0,0,0,0}, // 8 -> 1, 3
{0,0,1,0,1,0,0,0,0,0}}; // 9 -> 2, 4
--N;
while (N) {
if (N & 1) ans = mul(ans, M);
M = mul(M, M);
N >>= 1;
}
int sum = 0;
for (int i=0; i < 10; ++i)
sum = (sum + ans([0][i]) % kMod;
return sum;
}
};70. Climbing Stairs(Fibonacci sequence)
dp[i] = 1 * dp[i-1] + 1*dp[i-2]
dp[0] = dp[1] = 1, find dp[n]
| dp[i] dp[i-1] | = | dp[i-1] dp[i-2] | * | 1 1 |
| dp[i-1] dp[i-2] | | dp[i-1] dp[i-3] | | 1 0 |
| dp[n] dp[n-1] | = | dp[1] dp[0] | * | 1 1 | ^ (n-1) = | 1 1 | ^ n
| dp[n-1] dp[n-2] | | dp[0] dp[-1] | | 1 0 | | 1 0 |
class Solution{
public:
int climbStairs(int n){
auto mul = [](const vector<vector<long>>& A,
const vector<vector<long>>& B) {
const int m = A.size();
const int n = B.size();
const int p = B[0].size();
vector<vector<long>> C(m, vector<long>(p));
for (int i = 0; i < m; ++i)
for (int j = 0; j < p; ++j)
for (int k = 0; k < n; ++k)
C[i][j] += A[i][k] * B[k][j];
return C;
};
vector<vector<long>> dp{{1, 1}, {1, 0}};
vector<vector<long>> M{{1, 1}, {1, 0}};
n -= 1;
while ( n ){
if (n & 1) dp = mul(dp, M);
M = mul(M, M);
n >>= 1;
}
return dp[0][0];
}
};790. Domino and Tromino Tiling
f[i] = f[i-1] + f[i-2] + 2*g[i-1],
g[i] = f[i-2] + g[i-1]
f[0] = f[1] = 1, g[0] = g[1] = 0, ans = f[n]
|f[i] | T | | f[i-1] | T | 1 1 0 | | f[n] | T | f[1] =1 | T | 1 1 0 | ^ ( n - 1)
|f[i-1]| = | f[i-2]| _ | 1 0 1 | ⇒ | f[n-1] | = | f[0]=1| _ |1 0 1 |
|g[i] | = | g[i-1] | |2 0 1 | | g[n] | | g[1] = 0 | 2 0 1|
class Solution {
public:
int numTilings(int N) {
constexpr long kMod = 1e9 + 7;
auto mul = [kMod](const vector<vector<long>>& A,
const vector<vector<long>>& B) {
const int m = A.size();
const int n = B.size();
const int p = B[0].size();
vector<vector<long>> C(m, vector<long>(p));
for(int i=0; i<m; ++i)
for(int j=0; j<p; ++j)
for(int k=0; k<n; ++k)
C[i][j] = (C[i][j], A[i][k]*B[k][j]) % kMod;
return C;
};
vector<vector<long>> dp{{1, 1, 0}};
vector<vector<long>> M{
{1, 1, 0},
{1, 0, 1},
{2, 0, 1}};
--N;
while(N){
if (N & 1) dp = mul(dp, M);
M = mul(M, M);
N >>= 1;
}
return dp[0][0];
}
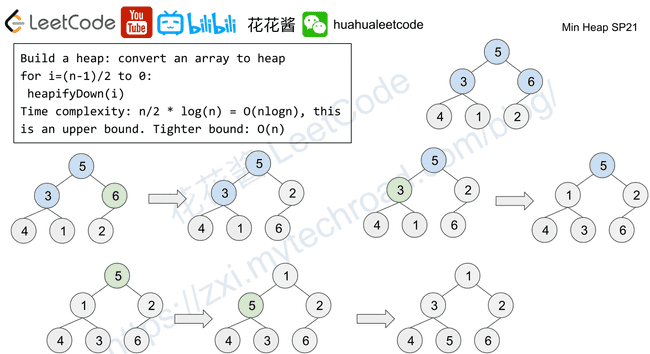
};SP21: Min Heap
“A heap is a specialized tree-base data structure which is essentially an almost complete tree that satisfies the heap
property” — wikipedia
Heap property (min heap): parent’s key is less than children’s key
#include <assert.h>
#include <iostream>
#include <vector>
using namespace std;
class MinHeap {
public:
// Return the min element.
int peek() const { return data_[0]; }
// Extract the min element.
int pop() {
// Swap the min element with the last one. O(1)
swap(data_.back(), data_[0]);
// Get the min element. O(1)
int min_el = data_.back();
// Evict the min element. O(1)
data_.pop_back();
// Maintain heap property. θ(logn)
heapifyDown(0);
return min_el;
}
// Add a new element to the heap.
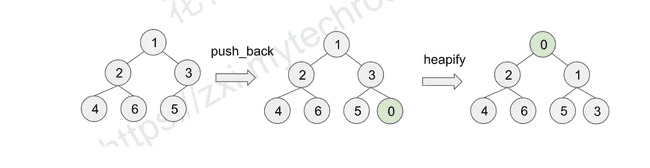
void push(int key) {
// Add the element to the end of the array. O(1)
data_.push_back(key);
// Maintain heap property. θ(logn)
heapifyUp(data_.size() - 1);
}
// Return the size of the heap.
int size() const { return data_.size(); }
private:
void heapifyUp(int index) {
// Stop at root.
if (index == 0) return;
int parent = (index - 1) / 2;
// Stop if greater or euqal to parent.
if (data_[index] >= data_[parent]) return;
// Swap with parent.
swap(data_[index], data_[parent]);
// Continue heapifyUp on parent.
heapifyUp(parent);
}
void heapifyDown(int index) {
int left = index * 2 + 1;
int right = index * 2 + 2;
// Stop if has no left child.
if (left >= data_.size()) return;
// Get the min child.
int min_child =
right < data_.size() && data_[right] < data_[left] ? right : left;
// Stop if less or euqal to min child.
if (data_[index] <= data_[min_child])
return;
// Swap with min child.
swap(data_[index], data_[min_child]);
// Continue heapifyDown on min_child.
heapifyDown(min_child);
}
vector<int> data_;
};
int main() {
vector<int> data{5,1,3,5,3,4,3,7};
MinHeap heap;
for (int x : data)
heap.push(x);
vector<int> output;
while (heap.size())
output.push_back(heap.pop());
assert(output == vector<int>({1,3,3,3,4,5,5,7}));
}heapifyUp
heapifyDown
Proof on O(n) time complexity
For a perfect tree of n nodes:
there are n/2 nodes of height 0
there are n/4 nodes of height 1
…
there are n/2^(h+1) nodes of height h
…
there is 1 node of height logn
For each subtree, it takes O(h) to heapify
1/2 + 2/4 + 3/8 + 4/16 + …
= 1/2 + 1/4 + 1/8 + 1/16 + … (1)
1/4 + 1/8 + 1/16 + … (1/2)
1/8 + 1/16 + … (1/4)
+ 1/16 + … (1/8)
…= 1 + 1/2 + 1/4 + 1/8 + … = 2
T = sum(n/2^(h+1) * O(h)) 0≤ h ≤ logn
= n _ sum(h/2^h) = n _ 2 = O(n)
class MinHeap:
def __init__(self, data = None):
self.data = list(data) if data else []
for i in range((len(self.data)) // 2, -1, -1):
self.heapifyDown(i)
def push(self, key):
self.data.append(key)
self.heapifyUp(len(self.data) - 1)
def pop(self):
self.swap(0, -1)
min_el = self.data.pop()
self.heapifyDown(0)
return min_el
def size(self):
return len(self.data)
def swap(self, i, j):
self.data[i], self.data[j] = self.data[j], self.data[i]
def heapifyDown(self, i):
smallest = i
for c in [2 * i + 1, 2 * i + 2]:
if c < self.size() and self.data[c] < self.data[smallest]: smallest = c
if smallest != i:
self.swap(i, smallest)
self.heapifyDown(smallest)
def heapifyUp(self, i):
if i == 0: return
parent = (i - 1) // 2
if self.data[i] >= self.data[parent]: return
self.swap(i, parent)
self.heapifyUp(parent)
def test():
data = [5,1,3,5,3,4,3,7]
heap = MinHeap()
for x in data: heap.push(x)
output = []
while heap.size():
output.append(heap.pop())
assert output == sorted(data)
def testBuildHeap():
data = [5,1,3,5,3,4,3,7]
heap = MinHeap(data)
output = []
while heap.size():
output.append(heap.pop())
assert output == sorted(data)
def main():
test()
testBuildHeap()
if __name__ == '__main__':
main()Applications:
- Heapsort O(nlogn)
- Dijkstra’s algorithm O(|E| log |V|)
- Priority Queue
- Selection algorithm
- Select top k elements among n
- Sorting: O(nlogn)
- Binary heap: O(n + klogn)
SP22: 动态规划/二分/分治
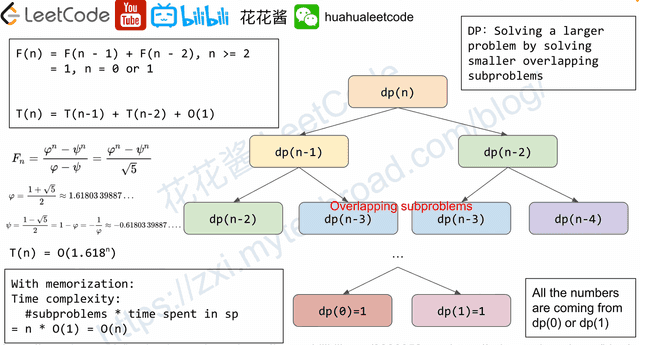
DP: Solving a larger problem by solving smaller overlapping subproblems
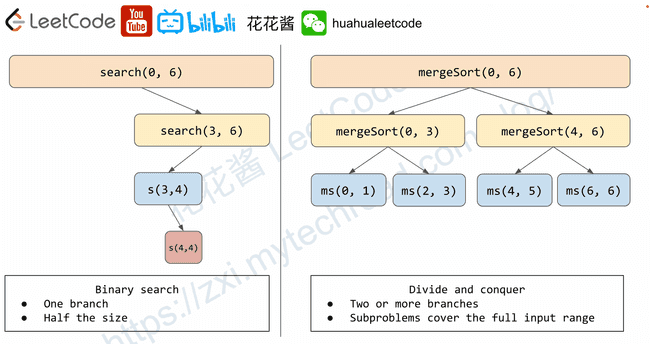
| Algorithmic paradigm | Branch(es) | Time complexity | Comments |
|---|---|---|---|
| Binary search | 1 | T(n) = T(n/2) + O(1) = O(logn), e.g. lower_bound | |
| logk*O(n) = O(klogn), e.g. guess and scan | Half in size | ||
| Divide and conquer | 2 |
2 Linear | T(n) = 2 * T(n/2) + O(n) = O(nlogn) e.g. mergesort T(n) = T(k) + T(n - k - 1) + O(1) = O(n) e.g. Tree ??? | Subproblems cover input range, no overlapping | | DP | Constant Linear Quartic | T(n) = T(n-1) + T(n-2)+ … +T(n-c) = nO(1)=O(n), T(n) = T(n-1) + T(n-2)+ … +T(n-k)=nO(k) = O(nk) T(n) = sum(T(1, i) + T(i+1, n)) = O(n^2)*O(n) = O(n^3) | Subproblem overlaps Memoization required for polynomial time complexity |
LeetCode 509 Fibonacci Number
Time compliexity:
Subproblems: n
Time in each subproblem: O(1)
T = n*O(1) = O(n)
Space complexity:
Subproblems: n
Space used by each subproblem: O(1)
S = n*O(1) = O(n)
class Solution:
@cache
def fib(self, n: int) -> int:
return n if n <= 1 else self.fib(n - 1) + self.fib(n - 2)LeetCode 55. Jump Game
Time complexity:
Subproblems: n
Time in each subproblem: O(k)
T = n *O(k) = O(nk)
Space complexity:
Subproblems: n
Space used by each subproblem: O(1)
S = n*O(1) = O(n)
class Solution:
def canJump(self, nums: List[int]) -> bool:
n = len(nums)
@cache
def dp(i: int) -> bool:
if i >= n - 1: return True
if i + nums[i] >= n - 1: return True
return any(dp(i + 1) for s in range(1, nums[i] + 1))
return dp(0)LeetCode 312. Burst Balloons
Time complexity:
Subproblems: O(n^2)
Time in each subproblem: O(n)
T = O(n^2)*O(n) = O(n^3)
Space comlexity:
Subproblems: O(n^2)
Space used by each subproblem: O(1)
S = O(n^2)*O(1) = O(n^2)
class Solution:
def maxCoins(self, nums: List[int]) -> int:
n = len(nums)
nums = [1] + nums + [1]
@cache
def dp(i: int, j: int) -> int:
if i > j: return 0
return max(dp(i, k-1)
+ nums[i-1] * nums[k] * nums[j+1]
+ dp(k+1, j) for k in range(i, j+1))
return dp(1, n)